Syntaktická analýza – Trocha teorie úvodem
Nedávno jsem se dostal k problému určení relativní atomové hmotnosti chemické sloučeniny (nebo její části) ze zadaného chemického vzorce. To je triviální problém, pokud ho řeší člověk. Jenže když chcete chemické vzorce vyhodnocovat strojově, tak to úplně jednoduché není. Tímto článkem bych chtěl odstartovat seriál, ve kterém chci ukázat, jak mi v řešení tohoto problému může pomoci syntaktická analýza.
- Syntaktická analýza – Trocha teorie úvodem
- Syntaktická analýza – Lexikální analyzátor
- Syntaktická analýza – Bezkontextová gramatika
- Syntaktická analýza – LL(1) parser
Syntaktická analýza – kde začít
Abych ten problém rozlousknul, budu muset vzorec nějak načíst, vyhodnotit jednotlivá slova vzorce (závorky, oddělovače, symboly prvků atd.), zvalidovat jestli vzorec vůbec dává smysl a nakonec vypočítat jednotlivé části vzorce ve správném pořadí. To jsou v teorii informatiky dobře známé a popsané úlohy.
Vzpomenul jsem na vysokoškolská studia a řekl si, že po XY letech opráším scripta z překladačů a teoretické informatiky. Šel jsem do toho po hlavě a skočil rovnou na tu správnou kapitolu s tím, že to za dvě hoďky rozseknu :-)). Omyl! Řeknu vám na rovinu, že když to člověk tolik let neviděl a skočí někam doprostřed, tak jsou ty vysokoškolská scripta docela výživné počtení.
Bez znalosti matematického aparátu, který jsem s radostí zapomněl a kterým se tam popisuje všechno, je pochopení i triviálních věcí celkem makačka. Příkladů málo, slovní popisy algoritmů bídné nebo žádné. Prostě se předpokládá, že vám to někdo vysvětlí na přednášce a cvičeních. Nakonec jsem to vyřešil, ale jak dlouho jsem to zkoumal tu radši ani psát nebudu.
Abych tedy odpověděl na otázku kde začít, tak dobrým startovacím bodem budou právě knihy/scripta věnované formálním jazykům, automatům, scripta z teoretické informatiky a samozřejmě scripta a knihy z překladačů. Doporučuji se také podívat na pojmy jako množiny a množinové operace bez kterých to nepůjde. Pro ty jež neměli to štěstí absolvovat informatiku na vysoké škole to nejspíš nebude úplně jednoduché čtení.
Problém: Výpočet atomové hmotnosti chemické sloučeniny
Čeho sem chtěl dosáhnout jsem nastínil už v předchozí kapitole. Problém je to na první pohled triviální. Postup výpočtu a pravidla jsou totiž dobře známá a pro člověka jednoduchá. Lidský mozek navíc dokáže jednoduše rozpoznat jednotlivé části vzorce, prioritu operátoru, závorky a další věci na základě zkušeností a nemusí aplikovat složité algoritmy. Prostě kouknete a vidíte.
Pro ověření výpočtu lze využít existující webové kalkulátory atomových hmotností Lenntech – Molecular Weight Calculator nebo Webqc – Molecular Weight Calculator.Pokud chci tedy vypočíst relativní atomovou hmotnost (Ar) jedné molekuly vody H2O vím, že mi stačí sečíst relativní atomové hmotnosti všech zastoupených prvků (atomů) ve sloučenině. Po dosazení do molekuly vody dostanu výraz 1,00794 x 2 + 15,9994 = 18,01528. Podobá se to vyhodnocení aritmetického výrazu. Ve výsledku to bude sice trochu složitější, protože nám do vzorce budou vstupovat závorky a oddělovače, které algoritmus trochu zkomplikují.
Příklady chemických vzorců
V tabulce níže uvádím příklady několika vzorců, kde je vidět použití závorek a oddělovačů. I když to není běžné, tak podle pravidel pro použití závorek, je asi dobré počítat i s tím, že ve vzorci budou i zbytečně uzávorkované části výrazu. Oddělovače slouží při vyhodnocení jako znak +. Oproti aritmetickému výrazu je v chemickém vzorci ještě jedna zvláštnost. Je to vidět ve vzorci MgSO4.7H2O která obsahuje za oddělovačem 7 molekul vody H2O a tedy 14 atomů vodíku H a 7 atomů kyslíku O. Ta sedmička, i když výraz za ní není v závorce, se vztahuje k celé molekule!
| MgSO4.7H2O | (MgSO4).(7H2O) | MgSO4.(7(H2O)) |
| MgSO4.(7)((H2O)) | K3[Fe(CN)6] | C6H2(NO2)3(CH3)3 – (TNT :-)) |
Trocha teoretické informatiky
Takže co s tím? No k problému se dá přistoupit asi vícero způsoby. Pro zjištění celkové hmotnosti by se dal asi použít převod na postfixovou notaci (reverzní polskou). Takový zápise se dá velice jednoduše strojově vyhodnotit pomocí zásobníku. Tento převod by se dal zrealizovat pomocí algoritmu shunting-yard, který byl navržen Edsgerem Dijkstrou. Algoritmus by se musel trochu upravit, ale to by neměl být nepřekonatelný problém.
K vyřešení mého problému to ale nestačí. Já potřebuji trochu těžší kalibr, protože potřebuji znát i výsledky jednotlivých částí vzorce. Takovým kalibrem je syntaktická analýza a syntaktický analyzátor nebo také parser. Parserů existuje poměrně hodně, podle toho jaké vstupy (jazyky) dokáží zpracovat a taky podle toho, jakým způsobem analýzu textu provádějí. Já se tu budu zabývat pouze jedním typem a tím bude LL(1) syntaktický analyzátor. Syntaktická analýza je ale pouze část řešení. Vstupem parseru je totiž seznam tokenů z lexikálního analyzátoru a množina pravidel (bezkontextová gramatika), podle které se dá vygenerovat z chemického vzorce syntaktický strom.
Než se pustím do syntaktické analýzy, bude dobré zlehka vysvětlit některé pojmy, protože se budou v textu často opakovat. K hlubšímu pochopení každého problému asi budete muset zabrouzdat do odborné literatury. Doporučuji scripta Úvod do teoretické informatiky a Teoretická informatika od pana Jančara viz zdroje.
Abeceda
Je libovolná konečná množina nějakých dohodnutých znaků (symbolů). Značíme ∑ (velké písmeno sigma) Např. ∑ = {a,b} je abeceda obsahující dva znaky a a b. V případě chemického vzorce se jedná o znaky ∑ = {A-Z, a-z, 0-9, ., -, (, ), [, ]}.
Slovo
Je libovolná konečná posloupnost symbolů složená ze symbolů nějaké abecedy ∑. Slovo w nad abecedou ∑ = {a,b} je například w = aabbaa. Délka slova: |w| = |aabbaa| = 6. Počet výskytů symbolu a ve slově: |w|a = |aabbaa|a = 4. ∑* je množina všech slov nad abecedou ∑. ∑+ je množina všech neprázdných slov nad abecedou ∑. ∑* = ∑+ ∪ {ε}. V mém případě budou slova jednotlivé zkratky chemických prvků, závorky, čísla a oddělovače.
Jazyk
Formální jazyk L je nějaká množina slov w nad abecedou ∑. Pro chemický vzorec to je L = L1 ∪ L2 ∪ L3 ∪ L4 kde:
L1 = {w ∈ {. , – }} = oddělovače
L2 = {w ∈ { (, ), [, ] }} = závorky
L3 = {w ∈ {[A-Z]{1}[a-z]{0,2}}| w ∈ P, kde P je množina všech zkratek z periodické soustavy prvků} = zkratky symbolů
L4 = {w ∈ { d+ }} = celá čísla
Konečný automat
Konečný automat (KA) je výpočetní model pro práci s formálními jazyky. Konečné automaty dělíme na deterministické (DKA) a nedeterministické (NKA). Konečné automaty se běžně zakreslují jako stavový diagram (graf automatu). Takový diagram se skládá z konečného počtu stavů a přechodů, které pro daný stav a přechod jasně udávají do jakých stavů se automat může posunout (přechodová funkce). Složitější automaty je možné zadávat přechodovou tabulkou, která je strojovému zpracování bližší. Formálně je konečný automat uspořádaná pětice A = { Q, ∑, δ, q0, F } kde:
- Q – je (neprázdná) množina všech stavů
- ∑ – je množina symbolů = vstupní abeceda
- δ – je přechodová funkce δ: Q x ∑ -> Q. Funkce δ(q, x) -> qx, která stavu q ∈ Q a znaku(přechodu) x ∈ ∑ přiřadí stav qx.
- q0 – je počáteční stav
- F – množina přijímajících stavů
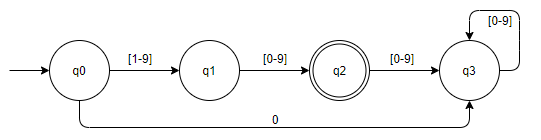
Příkladem takového automatu bude DKA přijímající jazyk celých čísel délky 2, které nesmí začínat nulou.
1 2 3 4 5 6 | KA = { Q, ∑, δ, q0, F } kde: Q = { q0, q1, q2, q3, q4 } ∑ - { 0-9 } - číslice 0-9 δ - zadána tabulkou dole q0 = q0 F = { q2 } |
| Stav | 0 | 1-9 | funkce 0 | funkce 1-9 | |
|---|---|---|---|---|---|
| -> | q0 | q3 | q1 | δ(q0, 0) -> q3 | δ(q0, 1-9) -> q1 |
| q1 | q2 | q2 | δ(q1, 0) -> q2 | δ(q1, 1-9) -> q2 | |
| <- | q2 | q3 | q3 | δ(q2, 0) -> q3 | δ(q2, 1-9) -> q3 |
| q3 | q3 | q3 | δ(q3, 0) -> q3 | δ(q3, 1-9) -> q3 |
Regulární jazyky a regulární výrazy
Regulární jazyk je takový jazyk, který se dá rozpoznat konečným automatem. Regulární jazyk není to samé co regulární výraz! Regulární výraz je formalismus (řetězec) pro popis regulárních jazyků. Formální zápisy regulárních výrazů jsou v teorii mírně odlišné od těch z praxe. Není třeba se toho děsit princip je stejný.
Bezkontextová gramatika (Context-free grammar, CFG)
Ne všechny jazyky lze popsat a rozpoznat konečnými automaty a je nutné použít silnější výpočetní model. Bezkontextová gramatika (G) je neformálně řečeno množina pravidel, podle kterých se dá vygenerovat věta z jazyka L nebo ověřit, jestli gramatika G danou větu přijímá (jestli je daná věta podle gramatiky správně). Formálně to je uspořádaná čtveřice G = { N, T, S, P } kde:
- N – je konečná množina neterminálních symbolů (proměnné). Dále v textu budu jako neterminály používat velká písmena.
- T – je konečná množina terminálních symbolů. V mém případě to jsou všechny slova z jazyka L. Důležité je, že N a T nesmí mít společné symboly tj. N ∩ T = ∅
- S – je startovací neterminál
- P – je množina přepisovacích pravidel ve formě A → β, kde A je neterminál a β je řetězec složený z terminálů a neterminálů.
Příkladem takové gramatiky budiž aritmetický výraz, kde je povolena pouze operace sčítání a násobení.
1 2 3 4 5 6 7 8 9 | G = { N, T, S, P } kde: N = {S} T = {+, *, a} S = S P = { S -> S + S, S -> S * S, S -> a } |
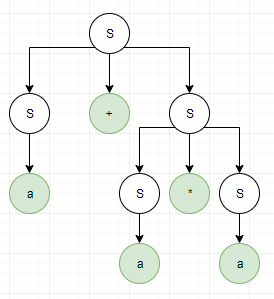
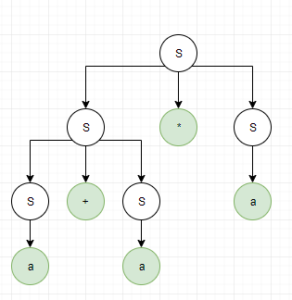
Pokud bych chtěl ověřit, že věta a + a * a je přijímána gramatikou G, musel bych provést její levou (nebo pravou) derivaci. S -> S + S | S * S | a. Levá derivace je vlastně odvození slova z počátečního neterminálu tak, že přepisuju vždy nejlevější neterminál, podle některého z pravidel. S => S + S => a + S => a + S * S => a + a * S => a + a * a. Došel jsem ke správnému výsledku, tudíž daná věta je přijímána gramatikou G. U pravé derivace přepisuju vždy nejpravější neterminál. S => S * S => S * a => S + S * a => S + a * a => a + a * a. Levý a pravý derivační(syntaktický) strom:
Závěr
Celá teorie kolem jazyků, konečných automatů a bezkontextových gramatik je podstatně složitější a vydá to i na několik knih. Cílem článku bylo dát pár vodítek a úvodní pohled na to, jak výše nastíněný problém řešit. Jednotlivým částem se ještě budu věnovat podrobněji. Konkrétně následující článek bude věnován lexikální analýze a konečným automatům.
Zdroje
- Scripta – Teoretická informatika – Doc. RNDr. Petr Jančar, CSc. ISBN 978-80-248-1487-2
- Scripta – Formální jazyky a automaty I – Černá, Křetínský, Kučera