Syntaktická analýza – Bezkontextová gramatika

Lexikální analyzátor z minulé části je hotový, ale než se pustím do syntaktické analýzy je třeba vyřešit ještě jednu věc. Do syntaktické analýzy kromě seznamu tokenů z lexeru vstupuje také něco, čemu se říká bezkontextová gramatika (obecně popsáno v části teorie). Gramatika je soubor pravidel, pomocí kterých se dá ověřit, že daná věta je správně. Formálně řečeno, že gramatika přijímá danou větu (slovo). Cílem tohoto článku je takový soubor pravidel navrhnout a upravit pro potřeby syntaktické analýzy.

Bezkontextová gramatika chemického vzorce

Začíná přituhovat. Na vyrobení bezkontextové gramatiky totiž neexistují žádné zázračné postupy. Prostě budete muset vzít tužku a papír a zkoušet. To se může stát docela těžkým úkolem, protože jak ověříte, že gramatika dělá to, co chcete? Jak ověříte, že vaše gramatika G přímá všechny slova vašeho jazyka? No těžko. Zaprvé většinou všechny slova neznáte a ani je nelze(většinou) vygenerovat. A zadruhé na to neexistuje žádný algoritmus ani důkaz. Prostě si musíte zkusit odderivovat nějaká slova a věřit, že to je v pořádku.

Doporučuju na to jít po částech. Vyřešit nejprve jednodušší gramatiky pro části výrazu, a nakonec je zkusit spojit dohromady. Velmi vám v tom může pomoct CFG Developer a LL1 parser generator. Tam si napíšete nějaké příklady vašeho jazyka a pak už jen sázíte gramatiku. Je to rozhodně rychlejší než to derivovat ručně.

Při výrobě gramatiky pro chemický vzorec můžete dojít například k něčemu takovému.  E -> (E) | [E] | EE | E.E | dE | Ed | s | d. Kde s je symbol z periodické soustavy prvků a d je číslo. Ač tato gramatika dělá skoro to co potřebuju, tak mi je nanic. Proč? Proto, že abych mohl použít LL(1) syntaktický analyzátor, musel bych se zbavit levé rekurze a faktorizace. Pokud se vám podaří napsat gramatiku, ale obsahuje výše zmíněné problémy, tak nastupují algoritmy pro jejich odstranění popsané zde a zde.

No a taky by ta gramatika musela být jednoznačná. Nejednoznačné gramatiky mají více levých derivací = více významů, a to strojovému zpracování moc nevoní. Bohužel algoritmus, který by vám řekl, že gramatika je jednoznačná nebo převedl gramatiku z nejednoznačné na jednoznačnou neexistuje. Ne každou gramatiku se vám podaří převést na LL(1).

Gramatika chemického vzorce

Mě se s tím moc párat nechtělo, a tak jsem vyšel z gramatiky pro aritmetický výraz, ze které jsem odstranil * a / a přidal separátory. Nakonec mi z toho vylezla jednoznačná gramatika G1, která sice dělá přesně to co potřebuju, ale není ve formátu LL(1). Jednoznačná gramatika nemusí být LL(1) ale každá LL(1) gramatika je jednoznačná.

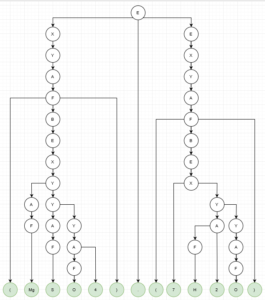
Ukázka levé derivace (MgSO₄).(7H₂O) podle G1

Otázka zní, jak udělat levou derivaci složitější věty, v případě, že mám více pravidel? V tuto chvíli nemám ještě žádný algoritmus a musím se řídit intuicí. Pokud dojdu do bodu, kdy již není možné pokračovat, musím se vrátit a zvolit jinou cestu. Pokud tedy budu derivovat (MgSO₄).(7H₂O) je mi jasné, že nejprve musím použít pravidlo E -> X . E a ne E -> X. V dalším díle ukážu, jak tento problém vyřešit algoritmicky.

E => X.E => Y.S => A.E => F.E => (B).E => (E).E => (X).E => (AY).E => (FY).E => (MgY).E => (MgAY).E => (MgFY).E => (MgSY).E => (MgSA4).E => (MgSF4).E => (MgSO4).E => (MgSO4).X => (MgSO4).Y => (MgSO4).A => (MgSO4).(B) => (MgSO4).(X) => (MgSO4).(7Y) => (MgSO4).(7AY) => (MgSO4).(7F2Y) => (MgSO4).(7H2Y) => (MgSO4).(7H2A) => (MgSO4).(7H2F) => (MgSO4).(7H2O)

Levý derivační strom chemického vzorce MgSO4.7H2O

Převod gramatiky na LL(1)

Přesto, že vám budou nástroje zmíněné výše tvrdit, že gramatika G1 je LL(1) tak není. Gramatika je LL(1) pokud nemá konflikty v parsovací (rozkladové) tabulce. Stačí si tedy tuto tabulku zkonstruovat (viz. další článek). Z ní byste se dozvěděli, že pro jeden neterminál a jeden terminál existuje v tabulce více přepisovacích pravidel. To je tzv. levá faktorizace nebo FIRST-FIRST konflikt. Poznáte ho tak, že pravá strana nějakého pravidla začíná stejným symbolem. V mém případě se jedná o pravidla:

E -> X.E | X
Y -> AY | A
A -> Fd | F

A ikdyž to není na první pohled zřejmé, tak i pravidlo B -> S | d, proto že S se dá přepsat podle pravidla S -> X -> dY. Zbavit se levé faktorizace je celkem jednoduché. Stačí pravé strany za společným znakem vytknout, za pravidlo s novým neterminálem. Z E -> X.E | X tak bude:

E -> X G
G -> .E | ε

Obdobným způsobem přepíšu i další pravidla. Problém mi dělá akorát pravidlo B -> S | d. Pro jednoduchost jsem se ho zbavil úplně :-). Z gramatiky mi tak vypadla možnost mít ve vzorci samostatně uzávorkované číslo např.: MgSO₄.(7)H₂O. No to asi přežiju :-). Kdyby to někdo upravil, tak se může pochlubit v komentáři. Výsledná gramatika G2 pak vypadá takto:

Zdroje

• Scripta – Teoretická informatika – Doc. RNDr. Petr Jančar, CSc. ISBN 978-80-248-1487-2
• Scripta – Formální jazyky a automaty I – Černá, Křetínský, Kučera
• http://www.mollypages.org/page/grammar/index.mp
• https://www.algoritmy.net/article/71/Transformace-na-LL1
• https://tomassetti.me/blog/